不明觉厉系列之 学霸数据党高能分析战士DPS输出

　　前情提要：[@AK-48] [[抛砖引玉]使用状态机和动态规划实现输出手法(以及APL)的自动生成]

　　AK-48这里已经解决了确定性的状态转移。我引入MDP解决了不确定状态转移(随机触发效果)。

　　由于一个状态执行相同动作可能会依概率转移到不同的后继状态，所以不再使用有向图来描述系统，而是使用[马尔可夫链]代替。

　　求解MDP与求解有向图相同，主导思想仍然是动态规划，但具体的方程有所区别。

确定性转移，有限视距

　　在有向图中，一个状态执行一个动作会确定地转移到一个后继状态。我们用来表示状态转移函数，其中s是当前状态，a是选择的动作，s'是后继状态。

　　描述这个系统不仅需要状态转移函数，还需要有收益函数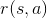，表示在s状态执行a动作得到的立即收益(对于DPS来说，就是造成的伤害)。

　　我们可以用值迭代法求解有向图。我们有值迭代方程：

　　式中A_s表示在当前状态s能够执行的动作集合。U_k(s)表示从s状态出发经过k步状态转移所能得到的最大收益。

　　依据此方程，可以进行值迭代法：

• 初始时将U₀置零，将k置零。
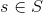• 对每一个状态，依据值迭代方程，计算U_k+1(s)的值。
• 将k递增后重复上一步，直到k足够大。

　　而此时在状态s下的最优策略，即执行使值迭代方程取值最大的动作a。

不确定性转移，有限视距

　　加入不确定状态转移后，后继状态与当前状态×动作不再是函数关系。我们用状态转移概率函数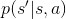来代替状态转移函数，此函数意义为在s状态执行动作a后到达后继状态s'的概率为p。

　　由于到达不同的后继状态可能得到不同的立即收益(例如那些由暴击触发的效果)，所以收益函数也会变为形如。

　　从s出发经过k步状态转移所能得到的最大收益，可以由从s向各个后继状态s'转移后得到的收益的依概率加权平均值(期望值)来表示。

　　此时值迭代方程为：

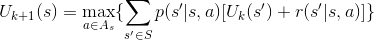
　　值迭代算法没有发生变化，与确定性状态转移的情况相同。

不确定性转移，无限视距

　　理想中的伤害输出过程是一个无限进行的过程，没有阶段转换(非斩杀->斩杀)，没有起始，也没有终结。上面的值迭代法都是经过固定的H步状态转移后就结束算法，而我们希望能够考察在无限的伤害输出过程中如何最大化DPS。

　　但由于伤害输出过程的累积收益(总伤害量)随时间流逝而无限增加，是发散的，所以我们引入一个衰减因子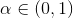使它收敛。

　　衰减因子的意义是在起始状态(t=0时)1点伤害的价值是1，而在进行一次状态转移后(t=1时)1点伤害的价值则视为α，进行两次状态转移后(t=2时)1点伤害的价值则视为α²。这样我们就能用一个收敛的数值来表示累积收益量。

　　此时值迭代方程变为：

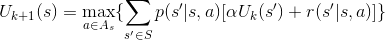
　　值迭代算法修改为：

• 初始时将U₀置零，将k置零。
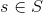• 对每一个状态，依据值迭代方程，计算U_k+1(s)的值。
• 如果U_k+1与U_k相等或差距小于容差，则认为算法已收敛，停止迭代。否则将k递增后重复上一步。

　　衰减因子α如果取得足够大，算法就会倾向于使长期收益(长期DPS)最大化。

收敛到DPS

　　上面的算法虽然对全程DPS进行了全面考虑，但较早时刻造成的伤害会得到较高的评价，而较晚时刻造成的伤害会得到较低的评价。这样如果衰减因子取得不恰当，算法会做出“杀鸡取卵”的决定，追求短期高伤害而损害长期利益。

　　如果采用动态的衰减因子，可以将累积收益收敛到DPS。那么算法必然将使DPS最大化，而无视这些伤害是在哪个阶段造成的。显然我们想要这种收敛方法。

　　这种收敛方法需要两个衰减因子α和β。值迭代方程为：

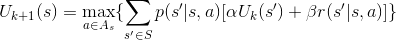
　　其中：

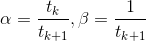
　　这样假如计算精度足够高，算法将忽视伤害发生的时刻，而只考虑伤害总量的大小。

实现

　　这里有一份狂暴战的实现 [https://github.com/AeanSR/maga/blob/master/mdp.cpp]，将模型简化(特别是缩小状态空间非常重要)，我们可以得到富有启发意义的结果。

　　运行后算法输出的结果是状态到动作的函数——列出所有合法的状态，并标注在这些状态下你应该执行的动作。

　　截取输出的一小部分如下：

　　RBST 0, BSST 0, ERRM 0, BTCD 0, RAGE 0 - bt 30252.371

　　RBST 1, BSST 0, ERRM 0, BTCD 0, RAGE 0 - bt 30560.494

　　RBST 2, BSST 0, ERRM 0, BTCD 0, RAGE 0 - bt 30862.881

　　RBST 0, BSST 1, ERRM 0, BTCD 0, RAGE 0 - bt 30522.141

　　RBST 1, BSST 1, ERRM 0, BTCD 0, RAGE 0 - bt 30829.566

　　RBST 2, BSST 1, ERRM 0, BTCD 0, RAGE 0 - bt 31130.418

　　RBST 0, BSST 2, ERRM 0, BTCD 0, RAGE 0 - bt 30790.562

　　RBST 1, BSST 2, ERRM 0, BTCD 0, RAGE 0 - bt 31095.748

　　RBST 2, BSST 2, ERRM 0, BTCD 0, RAGE 0 - bt 31380.145

　　RBST 0, BSST 0, ERRM 1, BTCD 0, RAGE 0 - bt 30278.369

　　RBST 1, BSST 0, ERRM 1, BTCD 0, RAGE 0 - bt 30586.496

　　RBST 2, BSST 0, ERRM 1, BTCD 0, RAGE 0 - bt 30888.879

　　RBST 0, BSST 1, ERRM 1, BTCD 0, RAGE 0 - ws 30592.404

　　RBST 1, BSST 1, ERRM 1, BTCD 0, RAGE 0 - ws 30909.021

　　RBST 2, BSST 1, ERRM 1, BTCD 0, RAGE 0 - ws 31202.273

　　RBST 0, BSST 2, ERRM 1, BTCD 0, RAGE 0 - ws 30860.826

　　RBST 1, BSST 2, ERRM 1, BTCD 0, RAGE 0 - ws 31176.746

　　RBST 2, BSST 2, ERRM 1, BTCD 0, RAGE 0 - ws 31467.826

　　从这一段结果我们可以看出，在同样怒气为零，嗜血可用的情况下，

　　如果没有激怒，你应该打嗜血

　　如果有激怒，血涌狂风>嗜血

MDP的优势

　　毕其功于一役，直接求取最优策略。理论性强。

　　所以对于能够采用MDP解决的小规模问题，MDP相比GA表现更好。

问题

　　MDP最大的问题是状态空间的维数灾难。每添加一个状态量，状态空间就需要多一维，于是状态空间的尺寸会失控。所以我们不能把精确的模型编制成MDP，只能做简化的模型。

　　另外，输出的是状态空间中每一个状态下应该执行的动作，类似一个策略字典，而非APL。这种输出虽然可以作为合法的APL提供给模拟器，但过于臃肿模拟器无法处理(这份实现的输出超过了3MB)。

　　人类也只能选择性地查阅其中感兴趣的部分，很难将输出全部阅读并理解。这也是MDP应用上的一大限制。